- Escogimos esta información como primera fuente porque no parece que tiene una gran variedad de información muy fácil de entender, y que nos muestra ilustraciones claras, también porque nos dan bases como comprobación de las leyes de kepler.
LEYES DE KEPLER por Nauta Programa Educativo Temático Tomo Física Ed. Zamora
Se deben destacar las precisas medidas realizadas por el astrónomo Tycho Brahe (1546-1601), teniendo presente que fue el último que hizo observaciones sin utilizar un telescopio y que elaboró un catálogo con la posición de unas 700 estrellas. Su colección de datos sirvió para que Johannes Kepler (1571-1630) enunciara sus tres leyes, que resumen las irregularidades observadas en el movimiento de los planetas:
Primera Ley: todos los planetas describen orbitas planas y elípticas que tienen al sol en uno de sus focos.
Segunda ley: los segmentos que unen al sol y a los planetas, barren áreas iguales en tiempos iguales
Tercera ley: los cuadrados de los tiempos empleados por los planetas en describir sus orbitas son directamente proporcionales a los cubos de los semiejes mayores.
Las tres leyes de Kepler constituyen la cinemática del movimiento planetario y, aunque reforzaron grandemente las teorías de Copernico, no se ocuparon de porque el movimiento era así y no de otro modo, ni la causa que lo provocaba.
RELACION ENTRE LEY DE GARAVITACION UNIVERSAL DE NEWTON Y LEYESDE KEPLER por Nauta Programa Educativo Temático Tomo Física Ed. Zamora
Isaac Newton mediante una sola hipótesis logró explicar las tres leyes de kepler y además demostró que los movimientos de los planetas y de los cuerpos que caían sobre la superficie de la tierra eran debidos al mismo tipo de causa. Anteriormente se consideraba que la tendencia de los cuerpos a caer sobre la tierra era una propiedad inherente a los cuerpos cercanos a su superficie. A partir de Newton, ya no se hablará más de mecánica celeste y terrestre, sino de una sola mecánica.
Comprobación de las leyes de Kepler:
Comos e ha dicho, la ley de la gravitación justifica las tres leyes de Kepler:Primera Ley: el hecho de que la fuerza gravitatoria que ejerce el sol sobre un planeta tenga la dirección del vector los une, demuestra que la órbita es plana.
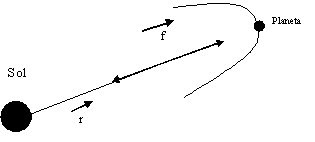
En efecto, al tener r y f la misma dirección, M = r y f = 0, luego M = dJ / dt = 0 y por tanto el momento cinético J, del planeta con respecto al Sol es constante: J = r y p. como es perpendicular en cada punto durante toda la trayectoria, esta trayectoria debe estar siempre en el mismo plano. Se puede demostrar que la orbita es elíptica, pero se omite porque es una demostración puramente matemática.
Segunda ley: en efecto, el área barrida en cierto intervalo de tiempo es constante.
El área triangulo A, barrida por la masa m2 en un pequeño desplazamiento r será:
Tercera Ley: esta ley se va a demostrar suponiendo trayectorias circulares, pues se simplifica el problema matemático. Sea un planeta de masa m, que se desplaza a una velocidad fija v, con lo que su aceleración centrípeta en un órbita de radio r será v²/r. Por tanto:
En concordancia con la tercera ley de Kepler. En resumen, se ha comprobado que las leyes de Kepler son válidas para sistemas de partículas en órbitas sometidas a fuerzas centrales, es decir, aquellas que tienen la misma dirección que la recta que une a las partículas.
- Escogimos esta como segunda fuente ya que nos muestran como son las leyes de kepler sencillamente, nos justifican los pensamientos de Kepler y además nos muestra algunos errores, sin embargo, no hay ilustraciones como en la primera fuente y no nos dan una comprobación.
LAS LEYES DE KEPLER por redescolar.ilce.edu.mx
A la muerte de Tycho Brahe, Kepler trabajó con el problema de la "determinación de la órbita de Marte". En un principio asumió que su órbita era circular, sin embargo, los parámetros que determinó, no coincidían con las posiciones de Marte en latitud, sobre todo cuando el planeta se encontraba más lejos del Sol, su conjetura de que la órbita de Marte era circular tampoco coincidía con las posiciones que se observaban cuando el planeta estaba en otros puntos del cielo, obteniendo discrepancias de hasta 8 grado cuando la precisión de las medidas de Tycho tenía un error de 1 grado. Estos errores implicaban que la órbita de Marte no era circular. Sus intentos por resolver el problema le llevaron entonces al estudio del movimiento de la Tierra. Como ya sospechaba, encontró que tampoco era uniforme respecto al centro de la órbita ni respecto al Sol.
En consecuencia a este descubrimiento introdujo la ley de las áreas.
2ª Ley de Kepler
La línea que une al Sol con el planeta, barre áreas iguales en tiempos iguales.
De este hecho se deducía que los planetas no viajaban siempre a la misma velocidad.
La permanencia de los errores en las posiciones de Marte, incluso después de introducir la velocidad variable, le llevó, finalmente, a no hacer ninguna suposición sobre la forma de la órbita. Después de la determinación de la distancia Sol-Marte en diversas posiciones, concluyó que la forma de la órbita era una elipse, uno de cuyos focos está ocupado por el Sol. Esto constituye la que después ha sido llamada su primera ley.
1º Ley de Kepler
Los planetas describen una orbita elíptica y el Sol está sobre uno de los focos de la elipse
Debe tenerse en cuenta que las elipses planetarias son muy poco excéntricas (es decir, la figura se parece mucho a una circunferencia) y la diferencia entre las posiciones extremas de un planeta son mínimas (a la máxima distancia de un planeta al Sol se denomina afelio y la mínima perihelio). La Tierra, por ejemplo, en su mínima distancia al Sol se halla a 147 millones de km, mientras que en su máxima lejanía no supera los 152 millones de km.
Errores de la segunda ley de Kepler:
· Considerar la velocidad del planeta en la órbita como inversamente proporcional a la distancia al Sol, en lugar de, como en realidad ocurre, como inversamente proporcional a la perpendicular desde el foco a la tangente a la órbita en el punto ocupado por el planeta.
· Kepler considera el área barrida por el radio vector como una medida válida de la suma de las distancias desde el foco a los sucesivos segmentos (360, en total) en que dividió la órbita, El propio Kepler era consciente de que tomar el área en lugar de la suma de las distancias era sólo una aproximación que hizo para facilitar los enormemente tediosos cálculos que se veía obligado a realizar para cada determinación de la posición del planeta.
Y por ultimo, la 3ª Ley
El cuadrado del período de revolución de cada planeta es proporcional al cubo de la distancia media del planeta al Sol.
La tercera ley permite deducir que los planetas más lejanos al Sol orbitan a menor velocidad que los cercanos; dice que el período de revolución depende de la distancia al Sol.
Es importante señalar que las leyes de Kepler no explican únicamente el movimiento de los planetas alrededor del Sol, sino que explican el movimiento de todos los astros y cuerpos del Universo.
- Escogimos esta información como tercera fuente ya que nos enseña las leyes de Kepler de una manera impractica y confusa, no hay ilustraciones sencillas y es más que todo muy monótono.
LEYES DE KEPLER por Wikipedia
Las leyes de Kepler fueron enunciadas por Johannes Kepler para explicar el movimiento de los planetas en sus órbitas alrededor del Sol. Aunque él no las enunció en el mismo orden, en la actualidad las leyes se numeran como sigue:
Primera Ley (1609): Todos los planetas se desplazan alrededor del Sol describiendo órbitas elípticas, estando el Sol situado en uno de los fo cos.
Segunda Ley (1609): El radio vector que une el planeta y el Sol barre áreas iguales en tiempos iguales
La ley de las áreas es equivalente a la constan cia del momento angular, es decir, cuando el planeta está más alejado del Sol (afelio) su velocidad es menor que cuando está más cercano al Sol (perihelio). En el afelio y en el perihelio, el momento angular L es el producto de la masa del planeta, por su velocidad y por su distancia al centro del Sol.
Tercera Ley (1618): Para cualquier planeta, el cuadrado de su período orbital (tiempo que tarda en dar una vuelta alrededor del Sol) es directamente proporcional al cubo de la distancia media con el Sol.
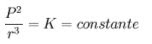
donde, P es el periodo orbital, r la distancia media del planeta con el Sol y K la constante de proporcionalidad.
Estas leyes se aplican a otros cuerpos astronómicos que se encuentran en mutua influencia gravitatoria como el sistema formado por la Tierra y la Luna.
Kepler dedujo sus leyes a partir de observaciones astronómicas precisas obtenidas por Tycho Brahe y, aunque sabía que explicaban el movimiento planetario observado, no entendía las razones de este comportamiento. La presentación de Kepler incorporaba una gran cantidad de detalles e incluso especulaciones metafísicas. Fue Isaac Newton quien extrajo de los escritos de Kepler la formulación matemática precisa de las leyes. Newton fue capaz de relacionar estas leyes con sus propios descubrimientos, dando un sentido físico preciso a leyes empíricas. El estudio de Newton de las leyes de Kepler condujo a su formulación de la ley de la gravitación universal.
La formulación matemática de Newton de la tercera ley de Kepler es:
donde, P es el
LEYES DE KEPLER RESUMEN:
LEYES DE KEPLER
¿Cuáles son las leyes de kepler?Las leyes de kepler son producto de una buena tarea de ordenamiento matemático por parte de Johanes Kepler de los datos recogidos por Tycho Brahe.
Primera ley: todos los planetas describen órbitas planas y elípticas que tienen al Sol en uno de sus focos.
Segunda ley: los segmentos que unen al Sol y a los planetas, barren áreas iguales en tiempos iguales.
A1 = A2 en igual tiempo
Tercera ley: los cuadrados de los tiempos empleados por los planetas en describir sus órbitas son directamente proporcionales a los cubos de los semiejes mayores.
T = período de la orbita T² = kr²Donde k es una constante
Las leyes de Kepler dieron una descripción del movimiento de los planetas alrededor del Sol pero no dieron una interpretación de las causas, interpretación que se daría años después
Isaac Newton logro explicar y comprobar las leyes de kepler tan solo con una hipótesis; y demostró que los movimientos de los planetas y de los cuerpos que caían sobre la superficie de la tierra eran debidos al mismo tipo de causa.
No hay comentarios:
Publicar un comentario